![]()
КИНЕМАТИКА ТВЕРДОГО ТЕЛА
Методические указания для иностранных студентов
УДК
531.01
Кинематика
твердого тела: Методические указания для иностранных студентов. - Ростов-н/Д: Рост.
гос. строит. ун-т, 2006 - 16 с.
Методические указания предназначены для работы с
иностранными студентами РГСУ, испытывающими трудности при записи лекций по теоретической механике. В них даны
основные определения, формулировки теорем, разъясняются трудные для усвоения
понятия. Рассмотрены типовые задачи.
Составитель О.В.
Явруян
Рецензент к.т.н. Д.А. Высоковский
1. ВВЕДЕНИЕ В
КИНЕМАТИКУ
1.1.Обобщенные
координаты. Число степеней свободы
При движении твердого тела отдельные его точки движутся в общем случае по
различным траекториям и имеют в каждый момент времени различные скорости и
ускорения. Однако имеются кинематические характеристики,
одинаковые для всех точек твердого тела.
Основные задачи кинематики твердого тела:
а) задать движение твердого тела, т.е. указать способ,
позволяющий определить положение тела в целом и каждой точки в отдельности в любой момент времени по отношению к выбранной системе координат;
б) определить
кинематические характеристики, присущие телу, а также указать способ нахождения траекторий, скоростей и
ускорений всех точек тела.
Не следует думать, что для движения твердого тела нужно задавать движение
каждой его точки. Это не так, ибо перемещения отдельных
точек связаны условиями неизменяемости расстояния между ними. Покажем, что положение свободного твердого тела определяется заданием шести независимых параметров. Возьмем в теле три не лежащие на одной прямой точки Ai(xi, yi, zi), i=1,2,3. Так как расстояния - l1, l2, l3
между точками A1, A2, A3 не изменяются, то девять координат связаны тремя зависимостями:
![]()
![]()
![]()
![]()
Следовательно,
независимых координат, определявших положение твердого тела, будет шесть. Если
твердое тело закреплено в какой-либо точке, то его положение будет
определяться только тремя координатами. Если тело закреплено в двух точках,
т.е. в теле имеется неподвижная прямая, проходящая через эти точки (например ![]() ), то из девяти
), то из девяти
координат остаются три координаты (![]() ), связанные двумя условиями:
), связанные двумя условиями: ![]() ,
, ![]() , т.е.
независимой будет одна координата.
, т.е.
независимой будет одна координата.
Независимые параметры, однозначно
определяющие положение твердого
тела в пространстве, называются обобщенными координатами.
Число обобщенных координат
называется числом степеней свободы.
1.2.Теорема о проекциях скоростей двух
точек твердого тела на ось, проходящую
через эти точки. Проекции скоростей двух точек твердого тела на ось,
проходящую через эти точки, равны между собой.
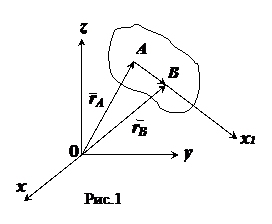 Доказательство: Обозначим радиус-векторы точек А
и В соответственно
Доказательство: Обозначим радиус-векторы точек А
и В соответственно ![]() и
и ![]() (рис.1)
(рис.1)
![]() ,
, ![]() . (1)
. (1)
Продифференцируем
равенство (1) по
времени, при этом учтем, что ![]() ,
, ![]() , получим
, получим
![]() . (2)
. (2)
Спроектируем
равенство (2) на ось ![]() , получим
, получим ![]()
Поскольку вектор ![]() и
и ![]() , т.о. вектора
, т.о. вектора ![]() и
и ![]() перпендикулярны, а
следовательно,
перпендикулярны, а
следовательно, ![]() перпендикулярен также и
оси
перпендикулярен также и
оси ![]() , т.е.
, т.е. ![]() , что доказывает теорему.
, что доказывает теорему.
2.
ПОСТУПАТЕЛЬНОЕ
И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Различают пять видов движения твердого тела: поcтупательное, вращательное, плоскопараллельное, сферическое и свободное
движение.
Поступательное и
вращательное движения являются простейшими.
2.1.Поступательное
движение
 Поступательным движением твердого тела называется
такое движение, при котором любая прямая, проведенная в теле, перемещается
параллельно самой себе.
Поступательным движением твердого тела называется
такое движение, при котором любая прямая, проведенная в теле, перемещается
параллельно самой себе.
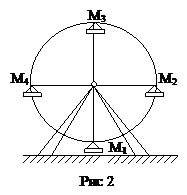
Приведем примеры
поступательных движений: кузов автомобиля на прямолинейном участке дороги
движется поступательно; движение кабин в аттракционе "Обозрение"
является поступательным (рис. 2) (любая прямая в кабине во время движения остается
параллельной своему первоначальному положению).
2.2. Основная
теорема поступательного движения. При поступательном движении все точки
тела описывают одинаковые траектории и имеют в каждый момент времени одинаковые
по модулю и направлению скорости и ускорения.
Для доказательства обратимся к формулам (1) и (2). Так как для поступательного
движения ![]() , то из (1)
следует, что траектории точек А и В при наложении совпадают, из (2) вытекают
равенства
, то из (1)
следует, что траектории точек А и В при наложении совпадают, из (2) вытекают
равенства ![]() и
и ![]() . Так как
точки А и В выбраны произвольно, то из найденных результатов следует, что у
всех точек тела их траектории, а также скорости и ускорения в любой момент
времени будут одинаковыми.
. Так как
точки А и В выбраны произвольно, то из найденных результатов следует, что у
всех точек тела их траектории, а также скорости и ускорения в любой момент
времени будут одинаковыми.
Из теоремы следует, что поступательное движение твердого тела вполне
определяется движением какой-нибудь одной его точки. Поэтому уравнениями
поступательного движения являются уравнения любой точки С
![]() . (3)
. (3)
При поступательном движении тела общую для всех его
точек скорость
![]() называет скоростью поступательного
движения, а ускорение
называет скоростью поступательного
движения, а ускорение ![]() - ускорением
поступательного движения. Векторы
- ускорением
поступательного движения. Векторы ![]() и
и ![]() можно изображать
приложенными в любой точке тела.
можно изображать
приложенными в любой точке тела.
Такие понятия как скорость тела,
ускорение тела имеют смысл только при поступательном движении. Если скорости
всех точек твердого тела равны между собой только для одного какого-либо
момента, то из этого не следует, что твердое тело движется поступательно. В
этом случае мы будем говорить, что твердое тело в данный момент имеет
мгновенную поступательную скорость.
2.3. Вращательное движение. Уравнение
вращательного движения
Если твердое тело движется так, что две его точки остаются неподвижными,
то движение тела называется вращательным, прямая АВ, проходящая через неподвижные
точки - осью вращения (рис.3). При вращательном движении траектории всех точек
- окружности, плоскости которых перпендикулярны к оси вращения, а центры лежат
на этой оси.
Для вращательного движения рассмотрим две задачи, указанные в пункте 1.1.
Рис.3
Положение твердого тела можно определить, задав координаты трех точек А,
В, М, не лежащих на одной прямой. Положение точек А и В нам
известно:
![]() ,
,
![]() ,
,
![]() ; положение тела будет определено, если мы будем знать в
любой момент времени положение точки М. Из трех координат этой точки
независимой будет только одна, так как расстояния АМ и ВМ постоянны.
Следовательно, положение твердого тела, вращающегося вокруг неподвижной оси,
определяется одним параметром. Тело имеет одну степень свободы.
; положение тела будет определено, если мы будем знать в
любой момент времени положение точки М. Из трех координат этой точки
независимой будет только одна, так как расстояния АМ и ВМ постоянны.
Следовательно, положение твердого тела, вращающегося вокруг неподвижной оси,
определяется одним параметром. Тело имеет одну степень свободы.
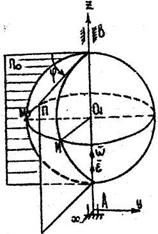
Определим положение вращающегося тела следующим образом. Проведем через
ось вращения Z две полуплоскости: неподвижную ![]() и подвижную П,
связанную с твердым телом и вращающуюся вместе с ним. Двугранный угол
и подвижную П,
связанную с твердым телом и вращающуюся вместе с ним. Двугранный угол ![]() между этими
плоскостями, отсчитываемый от неподвижной полуплоскости
между этими
плоскостями, отсчитываемый от неподвижной полуплоскости ![]() к подвижной П,
называется углом поворота тела. Будем считать угол
к подвижной П,
называется углом поворота тела. Будем считать угол ![]() положительным, если он
отложен от неподвижной полуплоскости в направлении против хода часовой стрелки
(для наблюдателя, смотрящего с положительного конца оси Z). Измеряется
угол
положительным, если он
отложен от неподвижной полуплоскости в направлении против хода часовой стрелки
(для наблюдателя, смотрящего с положительного конца оси Z). Измеряется
угол ![]() в радианах (1 рад.=
57° 17’44.88”). Угол поворота иногда выражается числом оборотов N. Тогда угол
в радианах (1 рад.=
57° 17’44.88”). Угол поворота иногда выражается числом оборотов N. Тогда угол ![]() в радианах,
соответствующий оборотам, определяется по формуле
в радианах,
соответствующий оборотам, определяется по формуле
![]() . (4)
. (4)
Угол ![]() определяет положение
подвижной полуплоскости, а также положение всего вращающегося тела. При
вращении тела угол поворота
определяет положение
подвижной полуплоскости, а также положение всего вращающегося тела. При
вращении тела угол поворота ![]() изменяется в зависимости
от времени
изменяется в зависимости
от времени
![]() .
(5)
.
(5)
Уравнение (5) называется уравнением
вращательного движения.
2.4. Угловая скорость и угловое ускорение
тела при вращательном движении
Для
изучения вращательного движения вводится
в рассмотрение угловая скорость ![]() , характеризующая быстроту изменения угла поворота
, характеризующая быстроту изменения угла поворота ![]() . Пусть за время
. Пусть за время ![]() тело повернулось на
угол
тело повернулось на
угол ![]() . Отношение
. Отношение ![]() называют средней
угловой скоростью тела за промежуток времени
называют средней
угловой скоростью тела за промежуток времени ![]() . Предел этого отношения, когда
. Предел этого отношения, когда ![]() стремится к нулю, называют угловой скоростью
тела в данный момент времени. Обозначая ее через
стремится к нулю, называют угловой скоростью
тела в данный момент времени. Обозначая ее через ![]() , получаем
, получаем
![]() ,
, ![]() . (6)
. (6)
Таким образом, угловая скорость тела в данный момент равна первой производной от угла
поворота тела по времени.
Угловая скорость
![]() может быть как
положительной, так и отрицательной. Знак
может быть как
положительной, так и отрицательной. Знак ![]() определяет направление
вращения тела:
определяет направление
вращения тела: ![]() , если угол
, если угол ![]() возрастает, т.е. тело
вращается против хода часовой стрелки,
возрастает, т.е. тело
вращается против хода часовой стрелки, ![]() , если
, если ![]() убывает, т.е. тeлo вращается по ходу часовой стрелки.
убывает, т.е. тeлo вращается по ходу часовой стрелки.
В общем случае угловая скорость зависит от времени ![]() , и для определения быстроты изменения
угловой скорости с течением времени, вводится понятие углового ускорения
, и для определения быстроты изменения
угловой скорости с течением времени, вводится понятие углового ускорения ![]() :
:
![]() .
(7)
.
(7)
Угловое ускорение может быть как положительным, так и отрицательным. Если
![]() возрастает, то
возрастает, то ![]() , если
, если ![]() убывает, то
убывает, то ![]() . Если модуль углового ускорения с течением времени
возрастает, то вращение тела называется ускоренным, а если убывает -
замедленным. При этом, если знаки
. Если модуль углового ускорения с течением времени
возрастает, то вращение тела называется ускоренным, а если убывает -
замедленным. При этом, если знаки ![]() и
и ![]() совпадают, то вращение
тела - ускоренное, если не совпадает - замедленное.
совпадают, то вращение
тела - ускоренное, если не совпадает - замедленное.
Вращение называется равномерным, если ![]() ,
, ![]() . Если
. Если ![]() в данный момент, то
это означает, что
в данный момент, то
это означает, что ![]() имеет экстремум в этот
момент времени. Если
имеет экстремум в этот
момент времени. Если ![]() , то вращение называется равнопеременным.
, то вращение называется равнопеременным.
В технике угловую скорость равномерного вращения обычно характеризуют
числом оборотов в минуту и обозначают эту величину через ![]()
![]() ,
, ![]() . (8)
. (8)
Легко
показать, что законы равномерного и равнопеременного вращательного движения
записываются в виде
![]() ;
(9)
;
(9)
![]() ,
(10)
,
(10)
где ![]() - соответственно
начальный угол поворота и начальная угловая скорость тела.
- соответственно
начальный угол поворота и начальная угловая скорость тела.
Угловая скорость равномерного вращательного движения изменяется по закону
![]() .
(11)
.
(11)
Угловую скорость тела можно также изобразить в виде вектора ![]() , где
, где ![]() - единичный вектор оси
вращения;
- единичный вектор оси
вращения; ![]() . Вектор
. Вектор ![]() направлен вдоль оси
вращения тела в ту сторону, откуда вращение видно происходящим против хода
часовой стрелки (рис.3). Такой вектор сразу определяет и модуль угловой скорости,
и ось вращения, и направление вращения вокруг этой оси.
направлен вдоль оси
вращения тела в ту сторону, откуда вращение видно происходящим против хода
часовой стрелки (рис.3). Такой вектор сразу определяет и модуль угловой скорости,
и ось вращения, и направление вращения вокруг этой оси.
Угловое ускорение тела можно также изобразить в виде вектора, направленного
по оси вращения. При этом направление вектора ![]() совпадает с
направлением вектора
совпадает с
направлением вектора ![]() , если тело вращается ускоренно и противоположно вектору
, если тело вращается ускоренно и противоположно вектору ![]() при замедленном вращении.
На рис. 3 показаны векторы
при замедленном вращении.
На рис. 3 показаны векторы ![]() и
и ![]() в случае ускоренного
вращательного движения.
в случае ускоренного
вращательного движения.
Угловую скорость и угловое ускорение часто изображают круговыми стрелками.
Круговая стрелка для угловой скорости показывает направление вращения, круговая
стрелка для углового ускорения - знак приращения алгебраической величины
угловой скорости.
Пример. В период разгона маховик вращается вокруг
своей оси по закону ![]() . Определить угловую скорость и угловое ускорение маховика в
тот момент, когда он сделает четыре оборота.
. Определить угловую скорость и угловое ускорение маховика в
тот момент, когда он сделает четыре оборота.
Решение. По заданному
закону вращательного движения находим угловую скорость и угловое ускорение
маховика в данный момент
![]()
Угол поворота маховика ![]() Найдем момент времени
Найдем момент времени ![]() , соответствующий этому углу из уравнения
, соответствующий этому углу из уравнения ![]() t=1 с.
t=1 с.
Угловая скорость и угловое ускорение маховика в этот
момент

Задание. Вычислите
угловую скорость вращения Земли вокруг своей оси.
Самые медленные вращения встречаются в звездном мире. Так, например,
период обращения Солнца вокруг центра галактики составляет 190 миллионов лет.
Наибольшая угловая скорость, полученная в технике, соответствует миллионам оборотов в минуту. С такой скоростью
вращаются гироскопы Гюгенара - маленькие роторы, подвешенные без подшипников в
магнитном поле.
 2.5. Скорости и ускорения точек вращающегося
тела
2.5. Скорости и ускорения точек вращающегося
тела
Рассмотрим какую-нибудь точку М вращающегося тела, находящуюся на расстоянии
h от оси вращения Z ( рис.3,4). При
вращении тела точка М будет описывать окружность радиуса h, плоскость которой перпендикулярна к оси вращения,
а центр ![]() лежит на самой
оси. Так как угловая скорость тела не зависит от выбора подвижной плоскости П,
то мы всегда можем выбрать эту плоскость так, чтобы она проходила через рассматриваемую
точку М. Будем определять положение точки М на её траектории дуговой
координатой S, отсчитываемой
от взятой на плоскости
лежит на самой
оси. Так как угловая скорость тела не зависит от выбора подвижной плоскости П,
то мы всегда можем выбрать эту плоскость так, чтобы она проходила через рассматриваемую
точку М. Будем определять положение точки М на её траектории дуговой
координатой S, отсчитываемой
от взятой на плоскости ![]() неподвижной точки
неподвижной точки ![]() , причем за положительное направление отсчета дуги S примем положительное направление отсчета угла
поворота
, причем за положительное направление отсчета дуги S примем положительное направление отсчета угла
поворота ![]() . Тогда
. Тогда ![]() , следовательно,
, следовательно,
![]() . (12)
. (12)
Эту
скорость точки М, в отличие от угловой скорости тела, часто называют линейной
скоростью.
Линейная скорость точки вращающегося твердого тела численно равна
произведению угловой скорости тела на расстояние от этой точки до оси вращения.
Вектор линейной скорости ![]() точки М расположен в
плоскости, перпендикулярной оси вращения, и направлен по касательной к окружности,
которую описывает точка М.
точки М расположен в
плоскости, перпендикулярной оси вращения, и направлен по касательной к окружности,
которую описывает точка М.
Для определения ускорения точки М воспользуемся формулами определения
ускорения точки при естественном способе задания движения
![]() (13)
(13)
![]() - тангенциальное (касательное) ускорение точки;
- тангенциальное (касательное) ускорение точки; ![]() - нормальное ускорение;
- нормальное ускорение;
![]() - радиус кривизны
траектории, равный h.
- радиус кривизны
траектории, равный h.
Из (13) находим, используя (12 )
![]() (14)
(14)
Касательное
ускорение ![]() направлено по
касательной к траектории (в сторону движения, если тело вращается ускоренно,
или в обратную сторону, если тело вращается замедленно).
направлено по
касательной к траектории (в сторону движения, если тело вращается ускоренно,
или в обратную сторону, если тело вращается замедленно).
Нормальное
ускорение всегда направлено по радиусу h к оси вращения (рис.4).
Чтобы определить направление вектора ![]() , достаточно вычислить угол
, достаточно вычислить угол ![]() , образуемый этим вектором с радиусом 01М.
, образуемый этим вектором с радиусом 01М.
Из рис. 4 ясно,
что ![]() . Так как угловая скорость
. Так как угловая скорость ![]() и угловое ускорение
и угловое ускорение ![]() являются
кинематическими характеристиками всего тела в целом, то из формул (14) следует,
что линейные ускорения всех точек вращающегося тела пропорциональны расстояниям
этих точек от оси вращения.
являются
кинематическими характеристиками всего тела в целом, то из формул (14) следует,
что линейные ускорения всех точек вращающегося тела пропорциональны расстояниям
этих точек от оси вращения.
В частном случае, когда тело вращается равномерно (![]() ), угловое ускорение
), угловое ускорение ![]() , поэтому
, поэтому ![]() ,
, ![]() . Следовательно, полное ускорение
. Следовательно, полное ускорение ![]() и направлено к центру
окружности, описываемой точкой.
и направлено к центру
окружности, описываемой точкой.
2.6. Векторные
формулы для определения скоростей и ускорений точек твердого тела, вращающегося
вокруг неподвижной оси
Докажем, что по величине и направлению вектор линейной скорости точки М
определяется формулой
![]() , (15)
, (15)
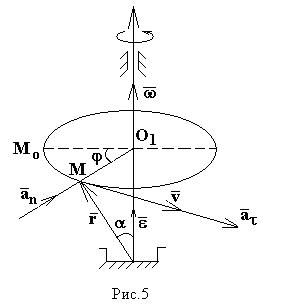 где
где ![]() - радиус-вектор точки
М относительно полюса, взятого на оси вращения. Формулу (15) называют формулой
Эйлера. Для доказательства найдем модуль и направление вектора
- радиус-вектор точки
М относительно полюса, взятого на оси вращения. Формулу (15) называют формулой
Эйлера. Для доказательства найдем модуль и направление вектора ![]() и сравним его
с вектором
и сравним его
с вектором ![]() . Учитывая, что
. Учитывая, что ![]() , получим
, получим ![]() ; следовательно
; следовательно ![]() ; вектор
; вектор ![]() перпендикулярен
к плоскости, проходящей через векторы
перпендикулярен
к плоскости, проходящей через векторы ![]() и
и ![]() , т.е. к плоскости, проходящей через точку М и ось
вращения, и направлен сторону вращения, т.е. совпадает с направлением вектора
скорости (рис.5).
, т.е. к плоскости, проходящей через точку М и ось
вращения, и направлен сторону вращения, т.е. совпадает с направлением вектора
скорости (рис.5).
Вектор ускорения точки М определяем как производную вектора скорости по
времени.
![]() . (16)
. (16)
Легко показать, что ![]() (17)
(17)
 Пример. Рейка 1, ступенчатое колесо 2 с радиусами
Пример. Рейка 1, ступенчатое колесо 2 с радиусами
![]() и
и ![]() и колесо 3 радиуса
и колесо 3 радиуса ![]() , скрепленное с валом радиуса
, скрепленное с валом радиуса ![]() , находятся
в зацеплении; на вал намотана нить с грузом 4 на конце (рис.6). Рейка движется
по закону
, находятся
в зацеплении; на вал намотана нить с грузом 4 на конце (рис.6). Рейка движется
по закону ![]() .
.
Определить угловые скорости и ускорения
всех колес, а также скорость и ускорение точки В.
Дано: ![]() м,
м, ![]() м,
м, ![]() м,
м, ![]() м, S1=
м, S1=![]() м.
м.
Определить: ![]() при t=1 с.
при t=1 с.
Рис.6
Решение. Механизм имеет одну степень свободы, поэтому для определения
кинематических характеристик указанных тел достаточно задать одну обобщенную
координату S1.
Рейка 1 и груз 4 совершают поступательное
прямолинейное движение, ступенчатые колеса 2 и 3 - вращательное движение
относительно неподвижных осей, перпендикулярных к плоскости чертежа и
проходящих через точки О1 и О2 соответственно. При решении задач учтем, что
когда два колеса находятся в зацеплении, скорость точки зацепления имеет у
каждого колеса одну и ту же величину.
Условимся обозначать скорости
точек, лежащих на внешних ободах колес через ![]() , на внутренних -
, на внутренних - ![]() .
.
Зная закон движения рейки 1,
находим её скорость ![]() .
.
Так как рейка 1 и колесо 2
находятся в зацеплении, то ![]() . Но колеса 2 и 3 тоже находятся в зацеплении. Следовательно,
. Но колеса 2 и 3 тоже находятся в зацеплении. Следовательно,
![]() или
или ![]() . Из этих равенств находим:
. Из этих равенств находим:
![]()
Вектор
![]() и направлен в сторону
положительной оси Ох. Вектор
и направлен в сторону
положительной оси Ох. Вектор ![]() и направлен в сторону
отрицательных значений Ох.
и направлен в сторону
отрицательных значений Ох.
Угловые
ускорения колес 2 и 3 находим по формулам:
![]()
Векторы ![]() совпадают по
направлению с векторами
совпадают по
направлению с векторами ![]() соответственно. Колеса
2 и 3 совершают ускоренные вращения. Для момента времени
соответственно. Колеса
2 и 3 совершают ускоренные вращения. Для момента времени ![]() сек получим :
сек получим : ![]() ;
; ![]()
Линейная скороcть точки В: ![]()
Линейное
ускорение точки В находится по формуле:
![]()
В момент времени t=1с находим ![]() м/с;
м/с; ![]() ;
; ![]() .
.
Задание. Найдите
дополнительно скорость и ускорение груза 4, а также законы движения колес 2 и
3.
3. СФЕРИЧЕСКОЕ
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
3.1.
Углы Эйлера. Уравнения сферического движения
Вращением твердого тела вокруг
неподвижной точки С (сферическим движением) называют такое движение, при
котором одна точка тела остаётся неподвижной во все время движения. Траектории
всех точек тела при таком движении
располагаются на поверхностях сфер, описанных из неподвижной точки.
Учитывая, что свободное твердое тело имеет шесть степеней свободы и
закрепление одной точки тела уменьшает число степеней свободы на три единицы,
получим, что при сферическом движении тело имеет три степени свободы. Три
независимых параметра, определяющих положение тела, можно задать различными
способами.
 Рассмотрим обобщенные координаты, введенные
Эйлером и называемые углами Эйлера. Эти углы обладают тем свойством, что через
них легко выражаются координаты любой точки тела.
Рассмотрим обобщенные координаты, введенные
Эйлером и называемые углами Эйлера. Эти углы обладают тем свойством, что через
них легко выражаются координаты любой точки тела.
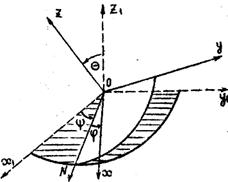
Через неподвижную точку О твердого
тела проведем неподвижную систему координат Оx1y1z1, относительно
которой будем рассматривать движение тела (риc.7).
Рис.7
Другую систему координат Оxyz скрепим с самим
телом, вращающимся вокруг неподвижной точки 0. Положение тела определится
положением подвижной системы координат относительно неподвижной. Пусть ON - линия узлов - прямая пересечения плоскостей x1y1z1 и xyz.
За положительное направление на линии узлов выбираем то её направление,
с которого поворот от оси Оz1 к оси Оz на наименьший угол виден происходящим против
часовой стрелки.
Угол
прецессии ![]() определяет положение
линии узлов относительно неподвижной координатной оси Ох1. Для
изменения этого угла тело должно вращаться вокруг неподвижной координатной оси
Оz1, которую называют осью прецессии. Угол
определяет положение
линии узлов относительно неподвижной координатной оси Ох1. Для
изменения этого угла тело должно вращаться вокруг неподвижной координатной оси
Оz1, которую называют осью прецессии. Угол
![]() считается
положительным, если он отсчитывается против часовой стрелки, если смотреть с
положительного направлении оси Оz1 (от оси Ох1
к оси ОN). Угол между линией ОN и осью Ох называется углом собственного
вращения. Для изменения угла
считается
положительным, если он отсчитывается против часовой стрелки, если смотреть с
положительного направлении оси Оz1 (от оси Ох1
к оси ОN). Угол между линией ОN и осью Ох называется углом собственного
вращения. Для изменения угла ![]() тело должно вращаться
вокруг оси Z, называемой
осью собственного вращения. Угол
тело должно вращаться
вокруг оси Z, называемой
осью собственного вращения. Угол ![]() считается положительным,
если он отсчитывается против хода часовой стрелки, если смотреть с
положительного конца оси Oz.
считается положительным,
если он отсчитывается против хода часовой стрелки, если смотреть с
положительного конца оси Oz.
Угол
![]() между плоскостями xOy и x1Oy1 лежит в плоскости zOz1. Он называется углом нутации. Для
изменения угла
между плоскостями xOy и x1Oy1 лежит в плоскости zOz1. Он называется углом нутации. Для
изменения угла ![]() тело должно вращаться
вокруг линии узлов. Угол
тело должно вращаться
вокруг линии узлов. Угол ![]() будет считаться
положительным, если он отсчитывается от оси Oz1 к оси Oz против хода
часовой стрелки, если смотреть с положительного направления линии узлов.
будет считаться
положительным, если он отсчитывается от оси Oz1 к оси Oz против хода
часовой стрелки, если смотреть с положительного направления линии узлов.
При
вращении тела вокруг неподвижной точки изменяются все три угла Эйлера. При этом
тело можно перевести из одного положения в другое, изменяя углы Эйлера не все
сразу, а последовательно, в любом порядке, начиная с любого угла.
Это позволяет утверждать, что углы Эйлера являются независимыми параметрами.
Чтобы задать уравнения сферического движения, нужно представить углы Эйлера как
непрерывные, однозначные функции времени
![]() (18)
(18)
Уравнения (18)
являются кинематическими уравнениями вращения тела вокруг неподвижной точки.
3.2. Теорема Даламбера-Эйлера
Чтобы представить себе наглядную геометрическую картину движения тела,
имеющего одну неподвижную точку, рассмотрим результат, сформулированный в
теореме Даламбера – Эйлера (1749-1750 г).
В каждый момент времени движение твердого тела вокруг неподвижной точки
можно рассматривать как вращение вокруг мгновенной оси, проходящей через эту
точку.
|
Рис.8 |
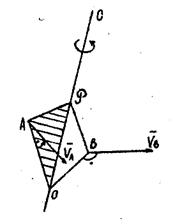
Для доказательства рассмотрим
две произвольнее точки А и В твердого тела (рис.8). Скорости этих точек в
данный момент обозначим соответственно ![]() и
и ![]() и предположим, что
и предположим, что ![]() не параллельно
не параллельно ![]() .
Проведем через точки А и В плоскости
.
Проведем через точки А и В плоскости ![]() и
и ![]() , перпендикулярные соответственно к скоростям
, перпендикулярные соответственно к скоростям ![]() и
и ![]() . Так как
точка О неподвижна, на основании теоремы о проекциях скоростей концов отрезка
на прямую, соединяющую эти точки, получим, что скорости точек А и В или равны
нулю (тело неподвижно), или
. Так как
точка О неподвижна, на основании теоремы о проекциях скоростей концов отрезка
на прямую, соединяющую эти точки, получим, что скорости точек А и В или равны
нулю (тело неподвижно), или ![]() ,
, ![]() . Следовательно, отрезки ОА и OB расположены в плоскостях
. Следовательно, отрезки ОА и OB расположены в плоскостях ![]() и
и ![]() . Поэтому плоскости
. Поэтому плоскости ![]() и
и ![]() , проходящие через точки О, пересекутся по некоторой
прямой ОС. Выберем на этой прямой произвольную точку Р. На основании той же
теоремы скорость точки Р должна быть одновременно перпендикулярна к пересекающимся
плоскостям
, проходящие через точки О, пересекутся по некоторой
прямой ОС. Выберем на этой прямой произвольную точку Р. На основании той же
теоремы скорость точки Р должна быть одновременно перпендикулярна к пересекающимся
плоскостям ![]() и
и ![]() , что невозможно, следовательно,
, что невозможно, следовательно, ![]() в данный момент
времени. Так как точка Р выбрана произвольно, приходим к
заключению, что скорости всех точек тела, расположенных на прямой ОС, в данный
момент равны нулю.
в данный момент
времени. Так как точка Р выбрана произвольно, приходим к
заключению, что скорости всех точек тела, расположенных на прямой ОС, в данный
момент равны нулю.
Ось ОР называют мгновенной осью вращения. Итак, при движении твердого
тела, имеющего одну неподвижную точку, в каждый данный момент существует мгновенная ось вращения,
проходящая через эту неподвижную точку.
Отсюда
следует, что движение твердого тела вокруг неподвижной точки можно представить
себе как непрерывный ряд последовательных вращений вокруг мгновенных осей,
проходящих через неподвижную точку.
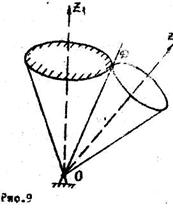 3.3.
Неподвижный и подвижный аксоиды
3.3.
Неподвижный и подвижный аксоиды
Геометрическое
место мгновенных осей вращения при движении тела образует в пространстве,
связанном с неподвижной системой отсчета, конус, называемый неподвижным
аксоидом (рис.9).
Рис.9
Кроме того,
мгновенная ось вращения при движении тела изменяет свое положение в
пространстве, связанном с телом, описывая коническую поверхность - подвижный
аксоид.
Рис.98
Подвижный и
неподвижный аксоиды имеют общую вершину в точке О, и в каждый момент времени
мгновенная ось вращения является общей образующей для подвижного и неподвижного
аксоидов (см. рис.9). Таким образом, подвижный аксоид при движении тела будет катиться по
неподвижному.
3.4.
Мгновенная угловая скорость и мгновенное угловое ускорение тела
Рис.1098
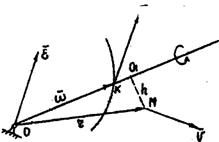 Угловая скорость
Угловая скорость ![]() , с которой
происходит элементарный поворот тела вокруг мгновенной оси вращения, называется мгновенной угловой скоростью.
Условимся вектор
, с которой
происходит элементарный поворот тела вокруг мгновенной оси вращения, называется мгновенной угловой скоростью.
Условимся вектор ![]() направлять по
мгновенной оси вращения в ту часть пространства, откуда вращение тела видно
против хода часовой стрелки (рис.10).
направлять по
мгновенной оси вращения в ту часть пространства, откуда вращение тела видно
против хода часовой стрелки (рис.10).
При движении тела вектор ![]() в общем случае
изменяется со временем и по модулю, и по направлению, т.е.
в общем случае
изменяется со временем и по модулю, и по направлению, т.е. ![]() . Будем называть вектором углового ускорения вектор,
характеризующий изменение в данное мгновение величины и направления угловой
скорости тела
. Будем называть вектором углового ускорения вектор,
характеризующий изменение в данное мгновение величины и направления угловой
скорости тела
![]() .
(19)
.
(19)
Направление
вектора ![]() совпадает с
направлением касательной
совпадает с
направлением касательной ![]() к годографу вектора
к годографу вектора ![]() (рис.10).
(рис.10).
Вектор ![]() будем также изображать
отложенным от центра О.
будем также изображать
отложенным от центра О.
3.5.
Линейные скорости точек тела при
вращательном движении вокруг неподвижной точки
Картина распределения скоростей в теле с
одной неподвижной точкой оказалась на данное мгновение такой же, как и в теле,
вращающемся вокруг неподвижной оси. Следовательно, линейные скорости точек тела
можно вычислить по векторной формуле Эйлера, только радиус-вектор каждой точки
удобно проводить из неподвижной точки (рис.10)
![]() .
(20)
.
(20)
Величина скорости v равна
![]() , (21)
, (21)
где h – кратчайшее
расстояние от данной точки до мгновенной оси.
Направлен вектор скорости точки M перпендикулярно
к плоскости, в которой находятся векторы ![]() и
и ![]() в сторону вращения.
в сторону вращения.
Из формулы (20) следует, что если ![]() , то
, то
![]() .
.
Применяя эту формулу последовательно к единичным
векторам подвижных осей (![]() ), получим формулы, которые носят название формул Пуассона
), получим формулы, которые носят название формул Пуассона
![]() (22)
(22)
3.6.
Линейные ускорения точек тела.
Пользуясь формулой Эйлера, найдем ускорение точки М
(рис.11).
![]() (23)
(23)
 Ускорение
Ускорение ![]() называют вращательным,
а ускорение
называют вращательным,
а ускорение ![]() - осестремительным
ускорением.
- осестремительным
ускорением.
Вектор ![]() направлен перпендикулярно
плоскости, проходящей через точку М и вектор
направлен перпендикулярно
плоскости, проходящей через точку М и вектор ![]() так, как было бы
направлено ускорение точки М, если тело вращалось бы вокруг оси, совпадающей с
так, как было бы
направлено ускорение точки М, если тело вращалось бы вокруг оси, совпадающей с ![]()
![]() ;
(24)
;
(24)
![]() - расстояние от точки
до вектора
- расстояние от точки
до вектора ![]() .
.
Вектор ![]() перпендикулярен
одновременно к
перпендикулярен
одновременно к ![]() и
и ![]() , т.е. направлен вдоль МС к оси вращения.
, т.е. направлен вдоль МС к оси вращения.
![]() . (25)
. (25)
Пример. Круглый конус, высота которого равна h, а угол при вершине - ![]() , катится по горизонтальной плоскости без скольжения так, что
его вершина О неподвижна, а центр основания С движется с постоянной по модулю
скоростью
, катится по горизонтальной плоскости без скольжения так, что
его вершина О неподвижна, а центр основания С движется с постоянной по модулю
скоростью ![]() (на рис.12 показано осевое сечение конуса
вертикальной плоскостью). Найти в данном положении
(на рис.12 показано осевое сечение конуса
вертикальной плоскостью). Найти в данном положении ![]() , а также скорость и ускорение точки В
конуса.
, а также скорость и ускорение точки В
конуса.
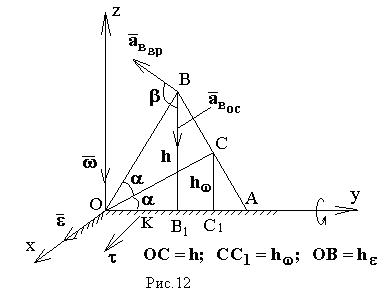 Решение. При качении без скольжения скорости всех точек образующей ОА равны в данный
момент нулю, следовательно, ОА - мгновенная ось вращения. Поверхность конуса -
подвижный аксоиод, горизонтальная плоскость
- неподвижный. Скорость
Решение. При качении без скольжения скорости всех точек образующей ОА равны в данный
момент нулю, следовательно, ОА - мгновенная ось вращения. Поверхность конуса -
подвижный аксоиод, горизонтальная плоскость
- неподвижный. Скорость ![]() перпендикулярна плоскости треугольника
перпендикулярна плоскости треугольника ![]() ,
, ![]() , предполагаем, что точка С движется к нам. Тогда вращение
конуса вокруг мгновенной оси ОА происходит против хода часовой стрелки.
, предполагаем, что точка С движется к нам. Тогда вращение
конуса вокруг мгновенной оси ОА происходит против хода часовой стрелки.
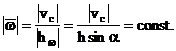 (а)
(а)
Поскольку ![]() , вектор
, вектор ![]() изменяется только по
направлению, вращаясь вокруг вертикали Oz с некоторой угловой скоростью
изменяется только по
направлению, вращаясь вокруг вертикали Oz с некоторой угловой скоростью ![]() . При этом конец
вектора
. При этом конец
вектора ![]() (точка К) описывает
окружность радиуса ОК в плоскости xy
(годограф
(точка К) описывает
окружность радиуса ОК в плоскости xy
(годограф ![]() ). Касательная к годографу вектора
). Касательная к годографу вектора ![]() перпендикулярна ОК.
Следовательно, вектор
перпендикулярна ОК.
Следовательно, вектор ![]() направлен по оси Ox
направлен по оси Ox
![]()
![]() (б)
(б)
Учитывая
(а) и (б), получаем ![]() .
.
Скорость
точки В находим по формуле ![]() .
.
(Скорость
точки В можно было найти из пропорции ![]() ).
).
Ускорение
точки В вычисляем по формуле ![]() .
.
![]() ;
; ![]()
![]() ;
; ![]()
Векторы
![]() лежат в плоскости
сечения ОАВ, причем
лежат в плоскости
сечения ОАВ, причем ![]()
![]() .
.