ДИНАМИКА ТОЧКИ
1.
Основные
законы динамики
Динамика представляет собой часть кинетики, посвященную
изучению движения материальных тел
(или вообще механических систем) в зависимости от действующих на них сил.
Движение тела определяется движением всех материальных точек (или
частиц), его составляющих; поэтому
естественно начать изучение динамики с изучения движения материальной
точки. Под материальной точкой мы понимаем
тело столь малых размеров, что различием в движении его частиц можно пренебречь. Материальную точку
можно рассматривать как точку
(геометрическую), имеющую массу. В дальнейшем часто для краткости материальную точку будем называть просто точкой.
В основе динамики
лежат законы, установленные путем обобщения результатов целого ряда опытов и наблюдений над движением тел и проверенные
обширной общественно-исторической
практикой человечества. Систематически эти законы были впервые изложены И. Ньютоном[1] в его классическом сочинении «Математические
начала натуральной философии», изданном
в 1687 г.
Первый закон (закон инерции), открытый Галилеем (1638
г.), гласит: изолированная от внешних
воздействий материальная точка
сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенные
силы не заставят ее изменить это
состояние. Движение, совершаемое
точкой при отсутствии сил, называется
движением по инерции.
Закон инерции
отражает одно из основных свойств материи — пребывать
неизменно в движении и устанавливает для материальных тел эквивалентность состояний покоя и движения по
инерции. Из него следует, что если F=Q, то
точка покоится или движется с постоянной по модулю и направлению скоростью (v = const); ускорение точки при этом равно нулю (w = Q); если же движение точки не является равномерным и прямолинейным, то на
точку действует сила.
Система
отсчета, по отношению к которой выполняется закон инерции, называется инерциальной
системой отсчета (иногда ее условно называют неподвижной). По данным
опыта, для нашей Солнечной системы инерциальной является система отсчета,
начало которой находится в центре Солнца, а оси направлены на так называемые
неподвижные звезды. При решении большинства технических задач инерциальной, с
достаточной для практики точностью, можно считать систему отсчета, жестко связанную с
Землей.
Второй закон (основной закон динамики) устанавливает, как изменяется скорость
точки при действии на нее какой-нибудь силы. Он гласит: производная по времени от количества движения
материальной точки равна действующей на нее силе. Другая ее формулировка: произведение массы материальной точки на ее
ускорение равно действующей на точку силе.
. (1)
Второй закон динамики, как и первый, имеет место только по отношению к инерциальной системе отсчета.
Из этого закона непосредственно видно, что мерой инертности материальной точки
является ее масса, так как две разные точки
при действии одной и той же силы
получают одинаковые ускорения только тогда, когда будут равны их массы; если же массы будут разные, то
точка, масса которой больше (т. е. более инертная), получит меньшее
ускорение, и наоборот.
Если на точку действует одновременно несколько сил, то они, как известно, будут
эквивалентны одной силе, т. е. равнодействующей R, равной геометрической сумме этих сил. Уравнение, выражающее основной закон динамики, принимает в этом
случае вид
или
. (2)
Этот же результат можно получить, используя вместо аксиомы параллелограмма закон
независимости действия сил, согласно которому при одновременном действии на
точку нескольких сил каждая из них сообщает точке такое же ускорение, какое она
сообщила бы, действуя одна.
Вес тела и его масса.
На все тела, находящиеся вблизи земной поверхности, действует сила тяжести Р, численно равная весу тела. Опытом установлено,
что под действием силы Р любое
тело при
свободном падении на Землю (с небольшой высоты и в безвоздушном пространстве) имеет одно и то же
ускорение g. Это ускорение, сообщаемое телу силой тяжести, называют
для краткости ускорением силы тяжести, или ускорением
свободного падения. Для этого движения на основании уравнения (2) имеем:
P=mg или
m =
(3)
Равенство (3)
позволяет определить вес тела, если известна его масса, и наоборот; оно устанавливает, что вес тела равен
его массе, умноженной на
ускорение силы тяжести, или масса
тела равна его весу, деленному
на ускорение силы тяжести. Вес
тела, как и величина g, изменяется
с изменением широты и высоты над уровнем моря;
масса же является величиной, для данного тела (или материальной точки)
неизменной.
2.
Задачи
динамики точки. Дифференциальные уравнения
Задачами
динамики точки являются:
1)
первая
задача динамики - зная закон движения материальной точки, определить, под действием
какой силы такое движение может происходить;
2)
вторая
задача динамики - зная действующие на
материальную точку силы, а также ее начальное положение и начальную скорость, определить закон движения точки. Вторая задача является в динамике основной.
Задачи динамики точки решаются с помощью соответствующих
дифференциальных уравнений,
связывающих координаты движущейся точки
с действующими на нее силами. Эти уравнения получаются из второго (основного) закона динамики. Представим уравнение
(2), выражающее второй закон Ньютона, в виде
,
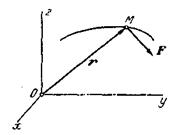
(4)
Рис. 1
где г —
радиус-вектор точки по отношению к инерциальной системе отсчета Oxyz (рис.
1), F = ΣFk —
равнодействующая приложенных
к точке сил. Уравнение (4) есть
дифференциальное уравнение движения свободной материальной точки в векторной форме.
Проектируя
обе части равенства (4) на оси Oxyz, получим дифференциальные
уравнения движения свободной материальной точки в прямоугольных декартовых координатах:
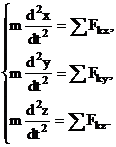(5)
2.1.
Решение первой задачи динамики
Задача состоит в том, чтобы, зная закон движения точки, т. е.
кинематические уравнения
x = x(t), y =
y(f), z = z(t), (6)
найти действующую силу, т. е.
Fx, Fy, Fz. Задача, как видим, легко решается с
помощью уравнений (5) и сводится к вычислению вторых производных по времени от
заданных функций (6).
Задача 1. Воздушный шар весом Р опускается с
ускорением w. Какой груз
Q (балласт) надо сбросить, чтобы шар стал
подниматься с таким же ускорением?
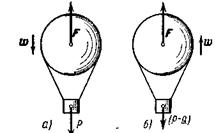Решение. На
падающий шар действуют сила тяжести Р
и подъемная сила F (рис. 2а).
Составляя уравнение (5) в проекции на вертикаль, получим
Рис.2
Когда
будет сброшен балласт (рис. 2б), вес шара станет равен Р-Q, а подъемная сила останется той же. Тогда,
учитывая, что шар при этом движется вверх, будем иметь:
,
исключая из этих уравнений неизвестную
силу F, найдем:
.
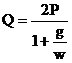Задача
2. Лифт весом Р (рис.3) начинает подниматься
с ускорением w.
Определить натяжение
троса.
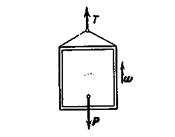Решение. Рассматривая
лифт как свободный, заменяем действие связи (троса) реакцией Т и, составляя уравнение (5) в
проекции на вертикаль, получаем:
.
Рис.3
Отсюда
находим:
.
Если лифт начнет опускаться с таким же
ускорением, то натяжение троса будет равно 
.
Решение второй (основной) задачи динамики
Эта задача состоит в том,
чтобы, зная действующую силу F, найти закон движения точки, т. е. кинематические уравнения (6).
Сила F может
вообще зависеть от времени, от положения
точки в пространстве
и от скорости ее движения, т. е. 
. Поэтому дифференциальные уравнения (5) будут в общем
случае иметь следующий вид:
(7)
Нахождение закона движения данной точки сводится к интегрированию системы (7), т. е. системы трех
совместных дифференциальных уравнений
второго порядка, в которых неизвестными функциями являются координаты
движущейся точки х, у, z, а
аргументом - время t. Проинтегрировав эту систему дифференциальных уравнений, получим х, у, z в функциях времени и шести произвольных
постоянных, т. е. найдем общее решение (общие интегралы) системы (7) в виде
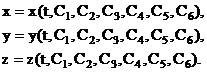(8)
Наличие в правых частях уравнений (8) произвольных постоянных указывает на то, что под действием данной силы
точка может совершать не какое-то
вполне определенное движение, а целый класс движений, имеющих разные законы при разных значениях постоянных Ci, i=1..6.
Физически этот результат объясняется тем, что точка, на которую начинает
действовать некоторая сила, будет двигаться по-разному в зависимости от
так называемых начальных условий, т. е. от начального положения и начальной скорости
этой точки. Например, движение свободной материальной точки под действием силы тяжести может быть
прямолинейным или криволинейным в зависимости от направления ее начальной скорости.
Чтобы сделать соответствующую задачу динамики определенной, надо кроме
действующих сил задать начальные условия, т. е. для некоторого момента времени t = t0 (начальный
момент) задать:
начальное положение точки 
и начальную
скорость точки 
3.
Прямолинейное движение точки
3.1. Дифференциальное
уравнение прямолинейного движения
Прямолинейное
(вдоль оси х) движение
свободной материальной точки определяется одним дифференциальным уравнением
второго порядка
и двумя начальными условиями:
(9)
при t = t0, 
3.2.
Основные этапы решения задач
Решение
задач динамики путем интегрирования соответствующих дифференциальных уравнений
движения сводится к следующим операциям.
1. Составление дифференциального уравнения движения.
Для этого надо:
а) выбрать начало отсчета (как правило, совмещая его с начальным положением точки) и провести координатную ось
вдоль линии движения, направляя ее,
как правило, в сторону движения; если под действием приложенных сил точка может находиться в каком-нибудь
положении в равновесии, то начало отсчета удобно помещать в положении статического равновесия;
б) изобразить движущуюся точку в произвольном положении (но так, чтобы
было x>0
и vx>0; последнее существенно, когда среди сил есть силы, зависящие от скорости) и
показать все действующие на нее силы;
в) подсчитать сумму проекций всех сил на координатную ось и подставить эту сумму в правую часть
дифференциального уравнения движения.
При этом надо обязательно все переменные силы выразить через те величины
(t, х или v), от которых эти силы зависят.
2. Интегрирование дифференциального уравнения движения производится методами, известными из курса высшей математики и зависящими от
вида полученного уравнения, т. е. от вида правой части в равенстве (9).
В тех случаях, когда на точку, кроме
постоянных сил действует одна переменная сила, зависящая только от
времени t, или только от расстояния х, или же только от скорости v, уравнение прямолинейного движения можно проинтегрировать методом разделения переменных.
3. Определение постоянных
интегрирования проводится
путем
удовлетворения полученных в п.2 решений
начальным условиям, составленных по данным
задачи.
Если дифференциальное уравнение движения является уравнением с разделяющимися
переменными, то вместо введения постоянных интегрирования можно брать сразу от обеих частей равенства определенные интегралы в соответствующих пределах.
4. Нахождение искомых в задаче величин и
исследование полученных результатов. Чтобы иметь возможность исследовать решение, а также произвести косвенную проверку результата
подсчетом размерностей, надо все решение проводить до конца в общем виде (в буквах), подставляя
численные данные только в
окончательные результаты.
Сделанные здесь общие указания относятся и к случаю криволинейного движения.
Рассмотрим три конкретные задачи, в которых сила зависит от времени, от расстояния
и от скорости движения точки.
3.3.
Сила зависит от времени
Задача
3. Груз весом Р начинает
двигаться из состояния покоя вдоль гладкой горизонтальной плоскости под
действием силы R,
величина которой растет
пропорционально времени по закону R = kt. Найти закон движения груза.
Решение. Выберем начало отсчета О в начальном
положении груза и направим ось Ох в сторону движения. Тогда начальные
условия будут: при t=0,
х=0, vx=0. Изображаем
в произвольном положении груз и действующие на него силы. В данном случае Rx=R=kt и уравнение (7) имеет вид 
Умножая
обе части равенства на dt, мы сразу
разделим переменные и, интегрируя,
получим: 
Подставляя сюда начальные данные, найдем,
что C1=0. Тогда, заменяя в полученном результате
, будем иметь:
.
Умножая обе части
этого равенства на dt,
мы опять разделим переменные и,
интегрируя, найдем:
.
Подстановка
начальных данных дает С2=0, и мы окончательно получаем закон движения груза в виде
.
Таким образом, проходимый грузом путь будет расти пропорционально кубу времени.
3.4. Сила зависит от
расстояния
Задача
4. Пренебрегая трением и
сопротивлением воздуха, определить, в
течение какого промежутка времени тело пройдет по прорытому сквозь Землю
вдоль хорды АВ каналу от его начала А до конца В (рис.4). При подсчете
считать радиус Земли R=6370 км.
Рис. 4
Указание. В
теории притяжения доказывается, что тело, находящееся внутри Земли,
притягивается к ее центру с силой F, прямо пропорциональной расстоянию r до этого центра. Принимая во внимание,
что при r=R (т. е. на поверхности Земли) сила F равна весу тела (F=mg),
мы получим,
что внутри Земли
где r=МС - расстояние от точки М до центра Земли.
Рис.4
Решение. Поместим начало отсчета О в середине хорды АВ (в этой точке тело, находящееся в канале, было бы в равновесии) и направим ось Ох вдоль линии ОА. Если обозначить длину хорды АВ
через 2а, то начальные условия задачи будут: при t=0, х=а, vx=0.
Рис.4
В произвольном
положении на тело действуют силы F и N. Следовательно,
так как из чертежа видно, что r cosα =x.
Действующая сила оказалась зависящей от координаты х точки М. Чтобы в этом случае в
дифференциальном уравнении движения разделились переменные, учтем, что
.
Тогда,
сокращая на m и
вводя обозначение 
, получим:
.
Умножая обе части
этого равенства на dx,
мы сразу разделяем переменные и,
интегрируя, находим:
.
По начальным
условиям при х=а, vx=0, следовательно, 
. Подставляя это значение, найдем:
.
Считая, что в рассматриваемом положении скорость направлена от М к О, т. е. vx<0, берем перед
корнем знак минус (легко, однако, проверить, что тот же
окончательный результат
получится и при знаке
плюс). Тогда, заменяя vx=
, имеем:
.
Разделяя переменные и интегрируя, получим:
Подставляя сюда
начальные данные (при t=0, х=а), находим, что С2=0. Окончательно закон движения тела в канале
будет иметь вид
.
Следовательно, тело будет совершать в канале АВ гармонические колебания с амплитудой
а.
Найдем теперь
время t1, движения тела до конца В канала;
в точке В координата х=а. Подставляя это значение в уравнение движения,
получим cos ktt= -1,
откуда kt1=π и tt = 
, учитывая введенное обозначение и произведя подсчет,
находим, что время движения по каналу АВ при
условиях задачи не зависит от его длины и всегда равно
Этот очень интересный результат породил ряд (пока еще фантастических) проектов прорытия
такого канала.
Найдем дополнительно, чему будет равна при движении максимальная скорость тела. Из выражения для vx видно, что v = vmax при x=0, т. е. в точке О. По величине
Если, например,
2а=0,1, R=637 км (приблизительно
расстояние от Москвы до Ленинграда), то vmax=395 м/с = 1422 км/ч.
3.5. Сила зависит от скорости
Задача 5. Лодку, масса которой m=40 кг, толкают, сообщая ей начальную
скорость v0 = 0,5 м/с. Считая силу сопротивления воды
при малых скоростях пропорциональной первой
степени скорости и изменяющейся по закону R=μv, где коэффициент μ=9,1 кг/с,
определить, через сколько времени скорость
лодки уменьшится вдвое и какой она за
это время пройдет путь. Найти также,
какой путь пройдет лодка до полной
остановки.
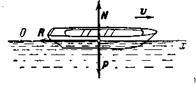Решение. Совместим
начало отсчета
О с начальным положением
лодки и направим ось Ох в сторону движения (рис.
5). Тогда начальные условия будут: при t =0, x =0, vx=v0.
Рис.5
Изображаем
в произвольном положении лодку и действующие на нее силы Р, N и R.
Для определения времени движения составляем дифференциальное уравнение (7), проектируя все действующие силы
на ось Ох. Замечая, что в данном случае vx=v, будем
иметь:
.
Проинтегрируем это уравнение, беря от обеих его частей после разделения
переменных соответствующие определенные интегралы. При этом нижним пределом
каждого из интегралов будет значение переменного интегрирования в начальный момент, а верхним -
значение того же переменного в произвольный
момент времени. Тогда, учитывая,
что по условиям данной задачи при t=0, v=v0, получим:
или 
Отсюда окончательно
(10)
Искомое
время t1 определим, полагая v=0,5v0. Это время, как видим, не зависит в данном случае от величины v0. Так
как In 2 = 0,69, то
Для определения пройденного пути целесообразнее вновь составить дифференциальное уравнение движения, так как
это уравнение позволяет сразу установить зависимость между x и v). Тогда получим:
Отсюда, сокращая
на v, разделяя переменные и учитывая, что при x=0, v=v0, будем
иметь:
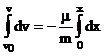или 
Следовательно, 
(11)
Полагая v=0,5v0, найдем искомый путь: 
м.
Чтобы найти путь, пройденный лодкой до
остановки, следует в равенстве
(11) положить v=0.
Тогда получим, что 
м.
Определяя время движения до остановки, мы из равенства (10) найдем, что при v=0 время t2=
. Это означает, что при принятом законе сопротивления (R=μv) лодка будет к своему конечному положению (определяемому координатой x2) приближаться асимптотически. Фактически же время движения лодки до остановки будет
конечным, так как с уменьшением скорости
закон сопротивления становится другим и соответственно изменяется вид
зависимости v от
t.
4. Криволинейное движение точки
4.1. Движение точки, брошенной под углом к
горизонту,
в
однородном поле тяжести
Изучим движение тела,
брошенного с начальной скоростью v0 под
углом α к горизонту, рассматривая его
как материальную точку массы m. При этом
сопротивлением воздуха пренебрежем, а поле тяжести будем считать однородным (Р=const), полагая, что дальность полета и высота траектории малы по сравнению с радиусом Земли.
Рис.6
Поместим начало
координат О в начальном
положении точки. Направим ось Оу вертикально
вверх; горизонтальную ось Ох расположим в плоскости, проходящей через
Оу и вектор vo, a ось 0z проведем перпендикулярно первым двум осям
(рис. 6). Тогда угол между вектором v0 и осью Ох будет равен α .
Рис.6
Изобразим
движущуюся точку М где-нибудь
на траектории. На точку действует одна только сила тяжести Р, проекции
которой на оси координат равны
.
Подставляя эти
величины в уравнения (7), после сокращения на m получим:
Умножая обе
части дифференциальных уравнений на dt и интегрируя, находим:
Удовлетворяя
начальным условиям, будем иметь:
Подставляя эти значения в найденные выше решения, придем к уравнениям:
Интегрируя
эти уравнения, получим:
Подстановка начальных данных
дает С1 = С2 = С3 = 0, и мы окончательно находим уравнения движения точки М в виде:
(12)
Из последнего уравнения следует, что
движение происходит в плоскости Оху. . .
Имея уравнения движения точки, можно методами кинематики определить все
характеристики данного движения.
1. Траектория
точки. Исключая из первых двух
уравнений (12) время t, получим
уравнение траектории точки:
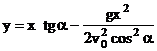(13)
Получили уравнение
параболы с осью, параллельной оси Оу.
Таким образом, брошенная под
углом к горизонту тяжелая точка движется
в безвоздушном пространстве по параболе.
2. Горизонтальная дальность. Определим горизонтальную
дальность, т. е. измеренное вдоль оси Ох расстояние ОС=Х. Полагая в
равенстве (12) у = 0, найдем точки пересечения траектории с осью Ох
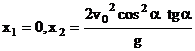
Следовательно, горизонтальная дальность
полета равна
Из
полученной формулы видно, что такая же горизонтальная дальность X будет получена при угле β, для
которого 2β=180°-2α, т. е. если угол β=90°-α.
Следовательно, при данной начальной скорости v0 в одну и ту же точку
С можно попасть двумя траекториями: настильной (α <45°) и навесной (β=90°-α > 45°).
При
заданной начальной скорости v0 наибольшая горизонтальная дальность в
безвоздушном пространстве получается, когда sin 2а=1, т. е. при угле α = 45°.
5. Высота траектории. Если положить в уравнении (13) 
, то
найдется высота траектории Н
6. Время полета. Из первого уравнения системы (12)
следует, что полное время полета Т определяется равенством Х=v0Tcosα. Заменяя здесь X его значением, получим
При угле
наибольшей дальности α*=45° все найденные величины равны:
Полученные результаты практически вполне
приложимы для ориентировочного определения характеристик полета снарядов (ракет), имеющих дальности порядка 200
600 км, так как при этих дальностях (и при 
45о) снаряд основную часть своего пути проходит в стратосфере, где сопротивлением воздуха можно
пренебречь. При меньших дальностях на
результат будет сильно влиять сопротивление воздуха, а при дальностях
свыше 600 км силу тяжести уже нельзя
считать постоянной.
7.
Задачи по пройденному
материалу
1. В шахте опускается равноускоренно лифт массой 280 кг.
В первые 10 с он проходит 35 м. Найти
натяжение каната, на котором висит лифт.
2. Материальная точка массой m=400 г совершает гармонические колебания по
горизонтальной оси Ox по закону 
([х]=см, [t]=с). Найти силу, действующую на точку как функцию от
х.
3. Груз весом Р=3000 кГ поднимается с ускорением 
м/с2. Определить натяжение каната, при помощи
которого поднимается груз.
4. Материальная точка массой m=0,5 кг совершает движение, согласно уравнениям:
определить величину и направление силы, действующей на
точку, в момент t=1 с.
5. Материальная точка М массой m движется прямолинейно по оси Ох. точка отталкивается
от неподвижного центра О силой F,
пропорциональной массе m и расстоянию
х, причем коэффициент пропорциональности равен k=4. Найти закон движения точки, если начальное
расстояние ее от центра О будет xo=5
м, vo=2 м/с.
6. Тело весом Р падает с некоторой высоты без начальной
скорости и испытывает сопротивление воздуха F=μv2, где μ – коэффициент сопротивления, v – скорость тела. Определить скорость тела: 1) как функцию времени и 2)
как функцию расстояния s.
7. Камень падает в шахту без начальной скорости. Звук от
удара камня о дно шахты услышан через 6,5 с от момента начала падения. Скорость
звука равна 330 м/с. Найти глубину шахты.
8. Тело массы m
вследствие полученного толчка прошло по негладкой горизонтальной плоскости за 5
с расстояние s=24,5 м и остановилось.
Определить коэффициент трения f.
9. За какое время и на каком расстоянии может быть
остановлен тормозом вагон трамвая, идущий по горизонтальному пути со скоростью
10 м/с, если сопротивление движению, развиваемое при торможении, составляет 0,3
веса вагона.
10.
Самолет летит
горизонтально. Сопротивление воздуха
пропорционально квадрату скорости и равно 0,5 Н при скорости 1 м/с.Сила тяги постоянна, равна 30760 Н и
составляет угол 10о с направлением полета. Определить наибольшую
скорость самолета.
11.
Тело массы 1 кг
движется под действием переменной силы F=10(1-t), где t – время
в с. Через сколько секунд тело остановится, если начальная скорость тела v0=20 м/с и
сила совпадает по направлению со скоростью тела? Какой путь пройдет тело до
остановки?
12.
Тяжелое тело
спускается по гладкой плоскости, наклоненной под углом 30о к
горизонту. Найти, за какое время тело пройдет путь 9.6 м, если в начальный
момент его скорость равнялась 2 м/с.
13.
В результате
полученного толчка кирпич начал скользить вниз с начальной скоростью v0=2 м/с по
неподвижной ленте конвейера, расположенной под углом α=30о к
горизонту. Определить путь, пройденный кирпичом за промежуток времени τ=2
с, если коэффициент трения скольжения кирпича о ленту конвейера равен f=0,4. Кирпич считать точечной массой.
14. Груз веса Р, находившийся в покое на гладкой
горизонтальной плоскости, начинает двигаться под действием горизонтальной силы,
проекция которой на направленную по горизонтали направо ось х равна Fx = H•sin(kt). Определить
закон движения груза, а также найти пройденный грузом путь через 2 с. от начала
движения в случае, когда H=2, P=10 H, k=π/6 рад/c.
15. В результате полученного толчка тело начало
подниматься вверх по наклонной поверхности, расположенной под углом α=60о
к горизонту с начальной скоростью v0=20 м/с. Коэффициент трения скольжения тела о
поверхность равен f=0,4. Определить путь, пройденный
телом до остановки.
16. Начальная скорость снаряда v0=490 м/с. Под каким углом α к горизонту следует
бросить этот снаряд из начала координат, чтобы он попал в точку с координатами x=700 м, y=680 м ?
17.
Определить угол
наклона ствола орудия к горизонту, если цель обнаружена на расстоянии 32000 м,
а начальная скорость снаряда v0=600 м/с. Сопротивлением воздуха пренебречь.
18.
Самолет летит на
высоте 4000 м над землей с горизонтальной скоростью 140 м/с. На каком
расстоянии х, измеряемом по горизонтальной прямой от данной точки, должен быть
сброшен без начальной относительной скорости
какой-либо груз для того, чтобы
он упал в эту точку? Сопротивлением воздуха пренебречь.
19.
Тело веса Р,
брошенное с начальной скоростью v0 по углом α к горизонту, движется под влиянием
силы тяжести и сопротивления R воздуха.
Определить наибольшую высоту h тела над
уровнем начального положения, считая сопротивление пропорциональным первой
степени скорости: R=kPv. Найти уравнения движения точки.
20.
Определить
движение тяжелой материальной точки, масса которой равна m, притягиваемой к неподвижному центру О силой, прямо
пропорциональной расстоянию. Движение происходит в пустоте; сила притяжения на
единице расстояния равно k2m; в момент t=0: 
, причем ось Oy направлена по
вертикали вниз.